宽度优先搜索小结

宽度优先搜索（Breadth First Search）通常是指图（树也是图）的一种查找顺序。它从某个节点开始，每次都遍历完当前节点可以直接到达的所有节点，再继续遍历下一层节点，一层一层的搜索。

二叉树的宽度优先搜索

例如我有一个二叉树：

      1
     / \
    /   \
   2     3
  / \   / \
 /   \ /   \
4    5 6    7

我的遍历顺序是1->2->3->4->5->6->7，这就是一种宽度优先搜索。通常树的宽度优先搜索会使用队列来辅助，具体可以看之前的这篇文章二叉树算法 - 广度优先遍历

树的宽度优先遍历通常用来解决

1. 深度先关问题
2. 需要层级遍历的问题（例如树的序列化和反序列化）

图的宽度优先搜索

图的基本表示方法

我们通常用2种方法来表示图：

1. 邻接矩阵(Adjacency Matrix)
2. 邻接表(Adjacency List)

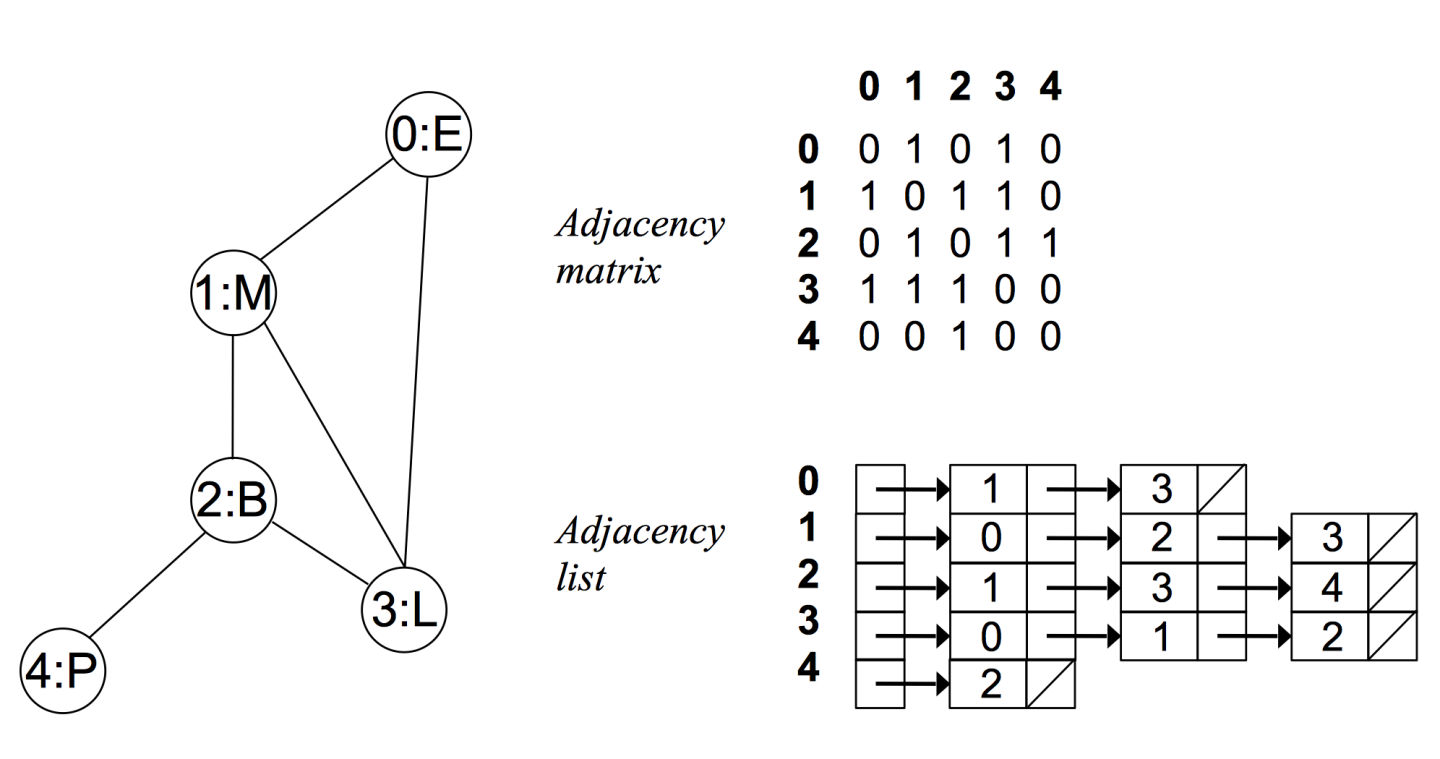
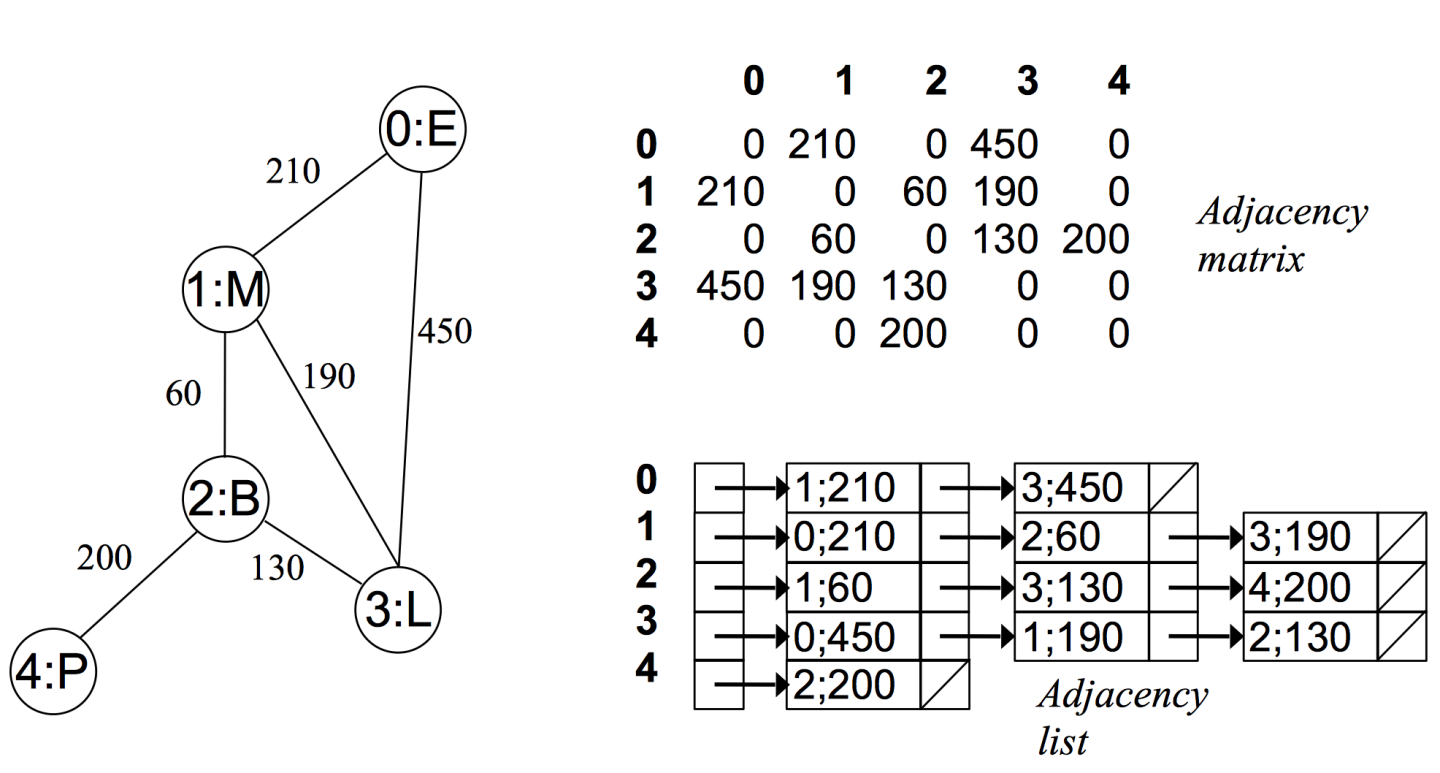
邻接矩阵

通常用二维数组来实现。

• 有 n 个节点的图需要有一个 n × n 大小的矩阵
• 在一个无权图中，矩阵坐标中每个位置值为 1 代表两个点是相连的，0 表示两点是不相连的
• 在一个有权图中，矩阵坐标中每个位置值代表该两点之间的权重，0 表示该两点不相连
• 在无向图中，邻接矩阵关于对角线相等

邻接表

通常用一维数组+链表来实现。

• 对于每个点，存储着一个链表，用来指向所有与该点直接相连的点
• 对于有权图来说，链表中元素值对应着权重

示例

无向无权图：

无向有权图：

有向无权图：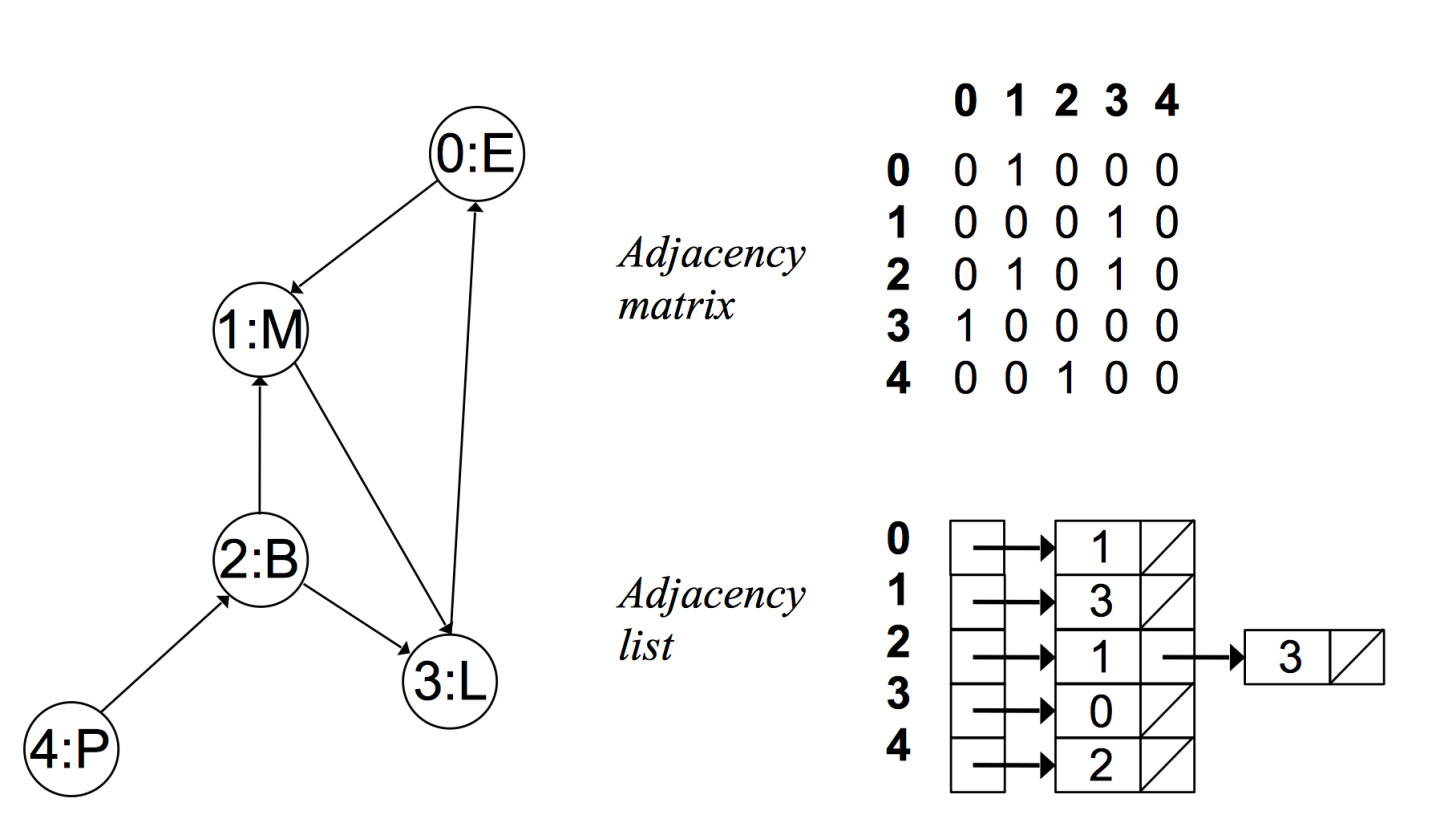

有向有权图：

基于无向有权图改一下就行了。

宽度优先搜索的常见问题

图的搜索算法中，经常会用到宽度优先搜索。例如图的层级遍历、在简单图中寻找最短路径、处理一些由点及面的问题、拓扑排序等，都合适用宽度优先搜索来解决。

• LeetCode 133. Clone Graph

  克隆图。可以采用宽搜，对原始图进行层级遍历。

// 这题还有很多其他方法，这里展示宽搜的方法
public Node cloneGraph(Node node) {
    if (node == null) {
        return null;
    }
    // 存放 <原始、复制> 节点的map
    HashMap<Node, Node> instances = new HashMap<>();
    // 存放已处理过邻居的节点，避免图中的环造成死循环
    HashSet<Node> processed = new HashSet<>();
    // 队列，用于宽度优先搜索
    Queue<Node> queue = new LinkedList<>();
    // 节点放入队列准备开始遍历
    queue.offer(node);
    // 存储对应的复制节点
    instances.put(node, new Node(node.val));
    // 开始宽搜
    while (!queue.isEmpty()) {
        Node origin = queue.poll();
        Node copy = instances.get(origin);
        // 如果节点没有处理过，且有邻居，开始复制邻居
        if (!processed.contains(origin) && origin.neighbors != null && origin.neighbors.size() > 0) {
            // 遍历邻居节点
            for (int i = 0; i < origin.neighbors.size(); i++) {
                Node neighbor = origin.neighbors.get(i);
                Node copyNeighbor;
                // 如果map中有，用已存在的实例，否则new一个新的，并放入map
                if (instances.containsKey(neighbor)) {
                    copyNeighbor = instances.get(neighbor);
                } else {
                    copyNeighbor = new Node(neighbor.val);
                    instances.put(neighbor, copyNeighbor);
                }
                copy.neighbors.add(copyNeighbor);
                // 将邻居节点放入队列，之后继续处理邻居节点的邻居们
                queue.offer(neighbor);
            }
        }
        processed.add(origin);
    }
    // 返回入参对应的复制节点
    return instances.get(node);
}

• LeetCode 210. Course Schedule II

  课程表。经典拓扑排序问题，可以用宽搜解决。
  拓扑排序的通用思路是：
  
  1.找出所有入度为0的节点，放入结果。
  
  2.将这些节点与邻居的边删除，这样它们的邻居的入度就会减少1。
  
  3.重复过程1，直到不能再继续。
  
  这时如果结果的数量与数据集数量一样，说明正常的完成了拓扑排序，否则说明有环，无法完成拓扑排序。

public int[] findOrder(int numCourses, int[][] prerequisites) {
    // 用于统计入度
    HashMap<Integer, Integer> indegree = new HashMap<>();
    // 邻接表，用于获取有哪些后继
    HashMap<Integer, ArrayList<Integer>> graph = new HashMap<>();
    // 统计入度并构造邻接表
    for (int i = 0; i < prerequisites.length; i++) {
        int parent = prerequisites[i][1];
        int child = prerequisites[i][0];
        // 统计入度
        indegree.put(child, indegree.getOrDefault(child, 0) + 1);
        // 构造邻接表
        if (graph.containsKey(parent)) {
            graph.get(parent).add(child);
        } else {
            ArrayList<Integer> list = new ArrayList<>();
            list.add(child);
            graph.put(parent, list);
        }
    }
    // 将入度为0的节点加入队列
    Queue<Integer> order = new LinkedList<>();
    for (int i = 0; i < numCourses; i++) {
        if (!indegree.containsKey(i)) {
            order.offer(i);
        }
    }
    // 用于存储结果
    ArrayList<Integer> result = new ArrayList<>();
    // 开始宽度优先搜索
    while (!order.isEmpty()) {
        int parent = order.poll();
        // 存入结果
        result.add(parent);
        // 通过邻接表中的找到所有邻居，并将它们的入度减少1，减少后如果变为0则放入队列用于下轮遍历
        if (graph.containsKey(parent)) {
            ArrayList<Integer> children = graph.get(parent);
            for (int i = 0; i < children.size(); i++) {
                int child = children.get(i);
                indegree.put(child, indegree.get(child) - 1);
                if (indegree.get(child) == 0) {
                    order.offer(child);
                }
            }
        }
    }
    // 结果少于预期数目，说明有环，无法完成
    if (result.size() != numCourses) {
        return new int[0];
    }
    // 将结果转换成数组返回
    int[] finalResult = new int[result.size()];
    for (int i = 0; i < result.size(); i++) {
        finalResult[i] = result.get(i);
    }
    return finalResult;
}

矩阵宽度优先搜索

涉及矩阵搜索的题目，宽搜也经常应用。此类题目视情况用宽搜或深搜，思路就是把它当成图来处理，只是把图中的节点的表示方法换成了矩阵中的横竖坐标表示。

• LeetCode 200. Number of Islands

  岛屿数量

public int numIslands(char[][] grid) {
    if (grid == null || grid.length == 0 || grid[0].length == 0) {
        return 0;
    }
    // 记录已经添加过队列的节点
    HashSet<String> alreadyInQueue = new HashSet<>();
    // 最终结果
    int islandCount = 0;
    // 开始逐行遍历，碰到'1'的节点时，通过宽搜，将它和它的所有邻居改成非'1'的值；
    // 然后继续遍历，每次找到'1'就意味着发现一个岛屿
    for (int i = 0; i < grid.length; i++) { // 行
        for (int j = 0; j < grid[i].length; j++) { // 列
            // 查找'1'
            if ('1' == grid[i][j]) {
                ++islandCount;  // 岛屿数量增1
                /*
                开始搜索grid[i][j]的所有邻居，直到无法找到'1'时，
                这里用递归方法写更简单，但这里给大家展示一下非递归的思路。
                */
                // 用于宽搜的队列
                Queue<SimpleEntry<Integer, Integer>> queue = new LinkedList<>();
                // 将发现的节点加入队列
                queue.offer(new SimpleEntry<>(i, j));
                // 采用这种方法可能碰到一个问题是，某个点是同一层节点的公共邻居，这样就会被重复添加到队列，
                // 所以这里用一个HashSet记录已经添加到queue中的节点，避免重复添加
                alreadyInQueue.add(i + "-" + j);
                // 开始宽搜
                while (!queue.isEmpty()) {
                    SimpleEntry<Integer, Integer> item = queue.poll();
                    int m = item.getKey();  // 行数
                    int n = item.getValue();// 列数
                    grid[m][n] = '2'; // 标记为1以外的char即可
                    // 上方的邻居
                    addToQueue(queue, alreadyInQueue, grid, m - 1, n);
                    // 右边的邻居
                    addToQueue(queue, alreadyInQueue, grid, m, n + 1);
                    // 下方的邻居
                    addToQueue(queue, alreadyInQueue, grid, m + 1, n);
                    // 左边的邻居
                    addToQueue(queue, alreadyInQueue, grid, m, n - 1);
                }
            }
        }
    }
    return islandCount;
}

private void addToQueue(Queue<SimpleEntry<Integer, Integer>> targetQueue, HashSet<String> alreadyInQueueFlag,
                        char[][] grid, int m, int n) {
    if (m >= 0 && m < grid.length && n >= 0 && n < grid[0].length
            && grid[m][n] == '1' && !alreadyInQueueFlag.contains(m + "-" + n)) {
        targetQueue.offer(new SimpleEntry<>(m, n));
        alreadyInQueueFlag.add(m + "-" + n);
    }
}

---

关于“图的基本表示方法”，参考来源：

• 数据结构与算法-图论
• Graph Algorithms